TETRIS. TECHNICAL
HANDBOOK.
The
classes contained in the program are:
-
CLASS APPLET
Method run ()
Cyclically, until the end of the game, it performs what
follows:
·
Calls the piece creation
procedure (implemented in the Tetrisgame class)
·
Calls the piece falling
procedure (implemented in the Tetrisgame class)
·
Calls the “game over”
control procedure
·
Set the piece falling speed
according to the level
Method update ()
This method is redefined so that the screen is not
cleaned up at every repaint( ) call. Doing so, we can paint the piece at the
new position while erasing the old one. This technique, along with double
buffering, is used in this program, in order to avoid the game flickering.
Method paint ()
·
At the achievement of a
fixed score, a message of level change is shown and the grid is cleaned up.
·
Paints the grid
·
Calls the method paint( )
(implemented in the Tetrisgame class)
·
If the game is over it
shows “GameOver”.
In this class some keyboard keys are catched. If the
pressed keys are 
the rotation (clockwise or anticlockwise sense) and
translation (right or left) procedures (implemented in the class Base) are
called.
-
CLASS TABLE
Once the piece is created it’s painted like a polygon; if
it can’t go down further since it would occupy busy areas or it would exit the grid, the piece becomes
part of the grid which contains already fallen pieces.
Pieces can be made of 4, 3, 2 or 1 little squares.
This class contains the structure of every little square:
an integer field that says if the little square is busy or not and 3 integers
giving the square color.
Method fill()
It sets the little
square color and makes it busy.
Method free()
It sets the little square color to Applet’s
background and frees it.
-
CLASS TETRISGAME
It creates the grid.
Method paint ()
It paints the piece
Method makePiece()
·
Choose a color in a random
way
·
In level 1 it creates a
piece choosing it randomly among all existing pieces
·
In level 2 it creates a
piece choosing it randomly among all pieces with 4, 3 or 2 little squares
·
In level 3 it creates a
piece choosing it randomly among all pieces with 4 or 3 little squares
·
In level 4 it creates a
piece choosing it randomly among all pieces with 4 little squares
-
CLASS BASE
It contains the procedures common to all pieces.
Method end ()
The game ends if just one little square is
busy in the first line
Method checkRows()
·
For every line of the
matrix it controls if it is full; if so, move downwards the grid overhanging
the matched line. In particular, for each little square in each row above the
matched one, if the square is busy give its color to the underneath little
square, while if it’s free sets it as free and assigns it the background color.
·
If it finds a full line,
the search for other full lines restarts from the first since the elimination
of a line and the consequent translation of the grid could have made other
lines to get completed.
Method anticlockwise_rotation()
·
Computes the rotation
coordinates
ROTATION
Every rotation of an angle j around the center C(x c ,y c ) of the
polygon can be executed through 3 steps:
1)
one translation from
the center C to the origin
[x’ y’ 1] = [x
y 1] T –1 where

2)
one rotation of an
angle j around the origin
[x’ y’ 1] = [x
y 1] R0 where
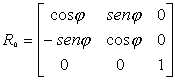
3)
one translation from
the origin to center C
[x’ y’ 1] = [x
y 1] T where
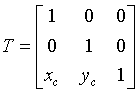
Therefore the rotation of an angle j
around the center of the polygon is obtained doing [x’ y’
1] = [x y 1] R
where

If j = 90° (anti-clockwise rotation with respect to the
axis origin which is in the top left corner) we obtain
[x’ y’
1] = [x y 1]
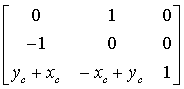
x’ = -y + yc
+ xc
y’
= x – xc + yc
·
Checks if the just computed
points exit the applet margins
·
Calls the right procedure
in class Piece# (specific for every piece) that controls if the new rotation
coordinates would occupy busy areas
·
The oldCoord vector
contains the piece’s coordinates which is to be erased, while coordCorr vector
contains the piece’s coordinates which
is to be painted. Therefore if the previous checks are positive, oldCoord will
be assigned the previously painted piece’s coordinates and coordCorr will hold
the new computed rotation coordinates.
The method is declared synchronized to avoid multiple
calls by other procedure that could mess up things (for example through signals
from keyboard); this is a way to make the method atomic.
Method clockwise_spin()
It’s quite similar to procedure
Ruota_antiorario ().
The only difference is that j = -90°(spin in hour sense
respect the origin of the aces that is found at the top left corner) and
therefore in the spin computation I obtain
[x’
y’ 1] = [x y 1]
= 
x’ = y – yc + xc
y’ = -x + xc
+ yc
Method traslation_right()
TRASLATION TOWARDS
RIGHT
x’
= x + a
y’
= y
[x’ y’ 1] = [x
y 1] 
The operations of this procedure are the same of those of the spin procedure.
Method traslation_left()
TRANSLATION TOWARDS LEFT
x’ = x –
a
y’ = y
[x’
y’ 1 ] = [x y 1] 
![]()
![]()
Method fallDownFast()
It continues to increase the vertical coordinates of the
piece until it does not find a busy positions or until the piece does not catch
up the applet bottom.
If it has found the busy positions, assigns like
coordinated to design those calculate ones to a previous step, while if it has
caught up the inferior limit, the calculate coordinates are those from
designed.
-
CLASS PEZZO0
It creates the piece, starting vertex and the center.
Method ifFallDown()
This method controls if the piece can fall down.
·
It checks if the piece it will occupy not free positions, falling
down.
·
If so, it calls the method
aggiornaGriglia()
·
If not so, the piece can
fall down, the coordinates y of the piece and the center are increased
Method updateGrid ()
·
It fills up the grid, calling the procedure fill() of the class
Table, passing the piece color as
parameter
·
Call the procedure
checkRows() of the class Base in order to check, once that the grill has been
dawned, if some line has been completed
Method checkNewCoord ()
·
It checks if also a little
square that build up the piece, is not free
·
the procedure gives back
otherwise true if the piece occupies free positions, false otherwise
The
relative classes to other pieces behave in analogous way.