The original data
were taken from the repository of the Computer Graphics Laboratory of
Stanford University.
Our phylosophy is to develop algorithms that can solve general problems in a reasonable time. In particular multi-scale and local operations have been fully explore in conjuntion which sparse noisy data.
|
Multi-resolution 2.5D surfaces. The reconstruction of 3D models of human body parts from range data is different with respect to that of general objects as they do not exhibit sharp discontinuities. Following this consideration, HRBF models which implement locally adapted filters have been introduced and described in the 1997 paper on Neurocomputing . They are based on stacking grids of Gaussians one over the other, where each grid operates at a different scale. The grids are not filled with Gaussians but these are inserted only in those crossings where the residual error is greater than the digitising noise. This allows to achieve a uniform reconstruction error. The mesh is obtained as the sum of the output of the layers. You can learn more from the papers on 2000 IEEE Trans. on I&M and 2004 IEEE Trans. on Neural Networks (where the model is compared with Wavelets). It results a very efficient and fast tool which can operate in real-time; an evaluation on its implementation with digital architectures is reported in a 2001 IEEE Trans. on I&M paper. In the 2005 paper on IEEE Trans. on I&M it is shown how to obtain a good mesh from a HRBF surface. More recently we have developed an on-line version of the algorithm that is in press on IEEE Trans. on Neural Networks, 2010; a video of the algorithm behavior can be downloaded from here. In 2012 we have applied the same ideas on Support Vector Regression and derived an algorithm that can produce a regression of comparable quality in a reduced time (Bellocchio et al., IEEE Trans. on Neural Networks and Learning Systems, 2012). This work received also the second best prize (runner-up prize) at IJCNN2010. |
|
|
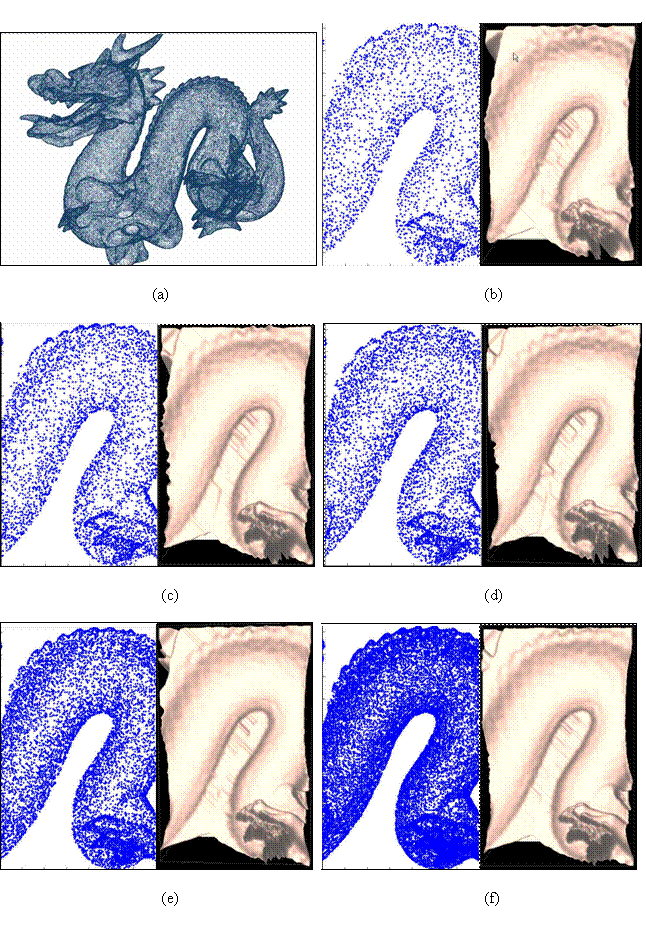
Filtering and reducing point clouds (IEEE Trans. NN 2006) . Modern scanners are able to deliver huge quantities of 3D data points sampled on an object's surface, in a short time. These data have to be filtered and their cardinality reduced to come up with a mesh manageable at interactive rates. We introduce here a novel procedure to accomplish these two tasks, which is based on an optimized version of soft Vector Quantization (VQ). The resulting technique has been termed Enhance d Vector Quantization (EVQ) since it introduces several improvements with respect to the classical soft VQ approaches, which are based on computationally expensive iterative optimization. Local computation is introduced here, by means of an adequate partitioning of the data space called Hyperbox, to reduce the computational time so as to be linear in the number of data points, N , saving more than 80% of time in real applications. Moreover, the algorithm can be fully parallelized, thus leading to an implementation that is sub-linear in N . The voxel side and the other parameters are automatically determined from data distribution on the basis of the Zador's criterion. This makes the algorithm completely automatic: because the only parameter to be specified is the compression rate, the procedure is suitable even for non-trained users. Results obtained in reconstructing faces of both humans and puppets as well as of artifacts from point clouds publicly available on the web are reported and discussed, in comparison with other methods available in the literature. EVQ has been conceived as a general procedure, suited for VQ applications with large data sets whose data space has relatively low dimensionality. |
| Last update: 31.07.2006 | For more information email here. |