AIS Lab - Free SW - RaIN Filter

[Download] AIS Lab - Free SW - A²C (Accelerometer Auto Calibration) [Download]

Accelerometer Auto Calibration (A²C) - abstract

Up to now, little attention has been posed on a principled derivation of the cost function used for autocalibration of MEMS triaxial accelerometers [1], [2]. Here we formulate the calibration problem in the context of maximum likelihood and we derive a general formulation that can be reduced to the classical quadratic cost function under certain hypotheses. We also use the Akaike Information Criterion to automatically determine the most adequate linear sensor model for the given calibration data set.

The adopted accelerometer model is linear and it is described as [1 - 4]:

v_n = V_CC (Sa-o) + n (1),

where v_n is the noisy output of the sensor (including the X, Y and Z channel), V_CC is the supply voltage, S is a 3x3 sensitivity matrix, a is the acceleration sensed by the accelerometer, o is the offset vector and n is the noise vector, which is assumed to be Gaussian. Sensor calibration consists in a procedure to estimate S and o from a set of measured data, such that Eq. (1) can be inverted and the acceleration a can be properly estimated.

Autocalibration is performed by minimization of a properly defined cost function. This is derived from the sensor model in Eq. (1) in the context of maximum likelihood estimate and considering that, in static condition, the module of the acceleration measured by the accelerometer is equal to g [1 - 4]. Considering N different sensor orientations, the following cost function can be considered:

F = sum_i=1..N[ (v_n,i /V_CC - o)^T S^-T S^-1(v_n,i /V_CC - o) - g² ]² (2),

where v_n,i represents the noisy output of the sensor in the i-th orientation. Minimization of F in Eq. (2) is performed by means of the Levemberg-Marquardt method, and it leads to the estimate of S and o.

Depending on the number of free elements in S and o in Eq. (1), sensor models with 2, 6, 9 or 12 parameters can be considered. In the proposed method, calibration is performed for each of these models; selection is the best model is then performed by means of the Akaike criterion, properly corrected to take into account the bias introduced by small dataset [1].

A large set of calibration results is presented in [1]. Here experiments on both simulated and real data show the effectiveness of the proposed approach, which guarantees higher accuracy with respect to more traditional calibration techniques like those in [2 - 4].

This software makes use of QT libraries dll (http://qt.nokia.com/products/) for the user interface, that is distributed by Nokia under LGPL licence.

Download

From here, you can download a compressed .rar file including a free copy of an executable (.exe) file which runs under Win 32 Platform (if you are interested in code compiled for different operative systems, please contact directly the authors by e-mail). In the same file, you'll find some calibration dataset too.

Instruction - installation

The executable file (and necessary DLLs) are all included in the compressed file. To install them, just decompress the .rar file in your directory. Then, to run A²C, just double click on A2C.exe.

Instruction - use of the A²C

To calibrate an accelerometer, you have to position it in N random orientation. For each orientation you have to measure the output of the accelerometer (in Volts) and save it in a text file with N rows and 3 columns; the i-th row of the text file will contain the X, Y and Z output of the accelerometer for the i-th orientation. Once you have created the file, you are ready to calibrate the accelerometer with A²C. Double click on A2C.exe. and the following GUI will appear:

In this GUI, you have to insert the voltage supply (VCC [V]), the noise standard deviation on each channel of the accelerometer (taken from it datasheet, in Volt - Sigma [V]) and the value of g. Then, load the data using the "Load data" button and indicating the text file with the accelerometer data and push the "Calibrate" button to calibrate the sensor.

Calibration is performed for sensor models with 2, 6, 9 and 12 parameters. Then, the best model is selected by the Akaike Information Criterion and the GUI appear as:

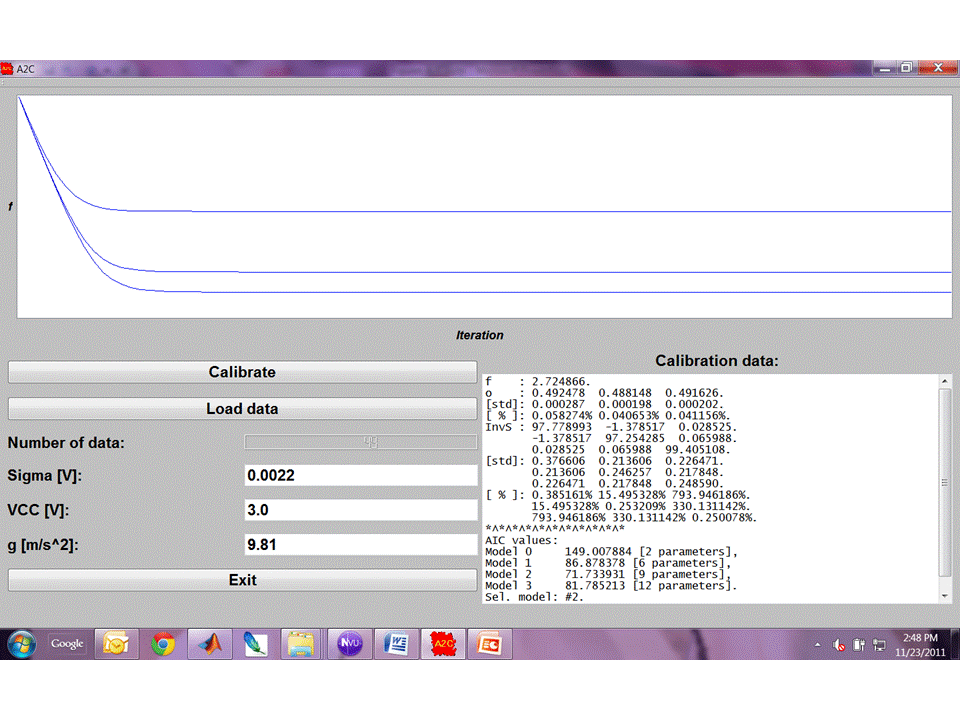
In the upper panel, the cost function as a function of the iteration is plotted for all the sensor models considered. In the lower panel on the right, calibration data are displayed. More in detail, you can observe the value of the cost function f for the best model selected and the values of o and S^-1 (InvS) for the same model. For each component of o and S^-1it is also shown the accuracy on the parameter, estimated by means of the covariance analysis; the corresponding percentage confidence of the parameter is also reported. Finally, the AIC indexes for the four models considered are also reported in this panel.

In the same directory of A2C.exe, you will also find a set of log files, that contain information on the estimated parameters for each sensor model considered by the present method.