AIS Lab - Free SW - RaIN Filter - 20th May 2011

Radiographic Impulsive Noise removal (RaIN) filter - abstract

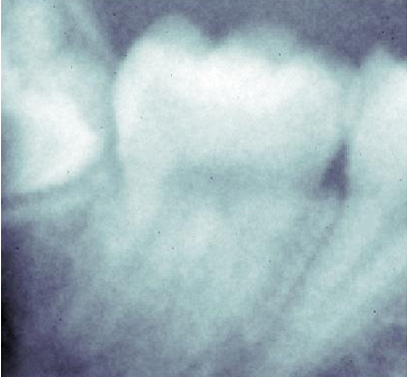
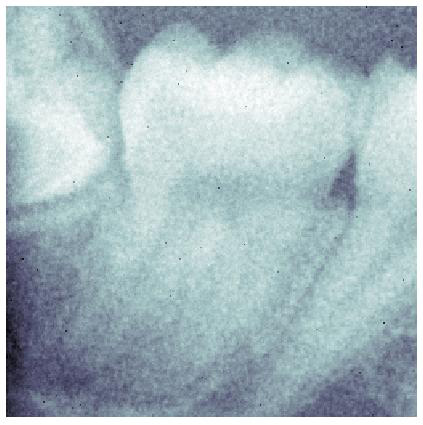
Digital radiographic images are corrupted by different kinds of noise. The major one has a Poisson statistic and it is associated with the photon counting process [1], [2], [3]; A/D conversion and data transmission constitute additional sources of noise; in particular, they can introduce impulsive noise [1], [2], [3]. Although impulsive noise can be poorly visible in the raw image (Fig. 1), its effect becomes dramatic when the image is manipulated (for instance though gamma transformation or unsharp masking) to increase the constrast and the visibility of the anatomical details (Fig. 2).


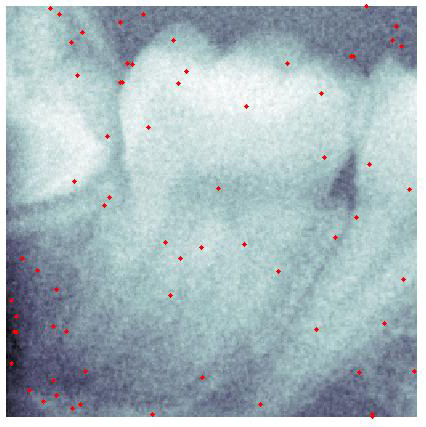
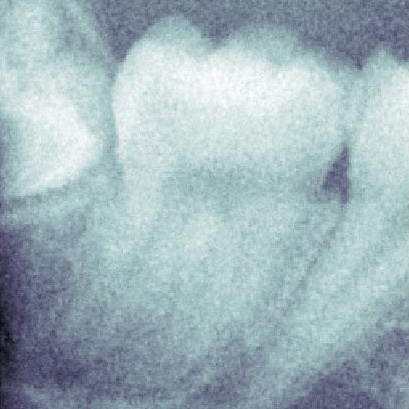
Figure 1. Zoom on a 256x256 pixel area from a typical panoramica radiography.


Figure 2. The same portion of a panoramic radiograph in Fig. 1 is shown here after treatment with unsharp masking; impulsive noise is clearly visibile here.

To avoid this undesiderable effect, impulsive noise has to be removed from the image before applying any processing algorithm. To this aim, we have proposed a new filter (called RaIN), based on a switching scheme, where all the pulses are first detected and then corrected through a median filter [1], [2]. The pulse detector is based on the hypothesis that the major contribution to image noise is given by the photon counting process, with only some pixels corrupted by impulsive noise. Such statistics is described by an adequate mixture model, which is used to identify the pixels corrupted by impusive noise (Fig. 3).


Figure 3. The pulses identified by the RaIN filter (in the image shown in Figs. 1 and 2) are indicated here by red points.


Figure 4. The same portion of a panoramic radiograph in Figs. 1-3 is shown here after treatment the RaIN filter and with unsharp masking; impulsive noise has been eliminated.


The filter is also able to reliably estimate the sensor gain. Its operation has been verified on both synthetic and real images; the experimental results demonstrate the superiority of the proposed approach in comparison with more traditional methods (Fig. 4).


Free SW - Download and instruction

Download

From this page, you can download a Matlab implementation of the RaIN filter (available here) and a test set of three images (each zipped in a .rar file):

    Test image 0: simulated image, sensor gain 0.2, impulsive noise rate 1% (available here).
    Test image 1: real cephalometric radiogaph, sensor gain approx 0.2, impulsive noise rate <1% (available here).
    Test image 2: real panoramic radiograph, sensor gain approx 0.1, impulsive noise rate <1% (available here).

Instruction - installation

The Matlab functions are included into a zipped .rar file. You just have to download and unpack it in your Matlab working directory.
Also the test images are zipped in a .rar file. Download the zipped files and unpack them in your Matlab working directory.

Instruction - use of the filter

First, load a radiographic image, corrupted by both Poisson and impulsive noise. For instance:

    NoisyImage = imread('NoisyImage.bmp');

Before filtering the image, be sure that the highest grey level is associated to the highest signal measured by the sensor (consider that, traditionally, radiographs are displayed as negative images - in this case, white is associated to the lowest signal - if you have a traditional radiograph, i.e. a negative image, you have to transform it before filtering - for instance, for a 12 bit image, you have to apply the transform:

    NoisyImage  = 4095 - NoisyImage;

before filtering it - notice that the constant term 4095 is equal to 2^12-1, where 12 is the number of bits of the image).

Now you are ready to filter the image. Just call the PoE_MM.m function:

    [Estg,EstG,EstPPoiss,EstImpulses]=PoE_MM(NoisyImage,NGreyLevels,G0,PPoiss0,PlotTime);

in input, there are the image to be filtered (NoisyImage), the number of grey levels of the image (NGreyLevels, 256 for a 8 bit image, 4096 for a 12 bit image and so on).
You also have to provide an initial guess for the sensor gain, G0, and for the probability of the Poisson noise, PPoiss0. If you have no idea for this values, you can use G0=1 and PPoiss0=0.99. The correct values of the sensor gain and Poisson noise rate will be then computed by the filter. A last input is the PlotTime variable: if this is 1, the Matlab script will show a figure with some information on the convergence of the filter - otherwise, no figure will be shown.
In output, you will obtain the image filtered by the RaIN filter (Estg), the estimates of the sensor gain (EstG) and of the Poisson noise rate  (EstPPoiss) and a binary image indicating the pulses found in the image by the filter  (EstImpulses).

Use of the Matlab code, including generation of simulated radiographs including impulisve noise, is also described in the HowDoesItWorks.m function.


For any further information, please contact:

Iuri Frosio, PhD
Computer Science Dept.
University of Milan
Via Comelico 39/41
+39 02 503 14010
frosio@dsi.unimi.it


References

[1] I. Frosio, S. Abati, N. A. Borghese, "Bayesian approach to impulsive noise removal in digital radiography," Int. Journal of CARS, Vol. 3, No. 1-2, Jun. 2008.
[2] I. Frosio, N. A. Borghese, "Statistical Based Impulsive Noise Removal in Digital Radiography," IEEE Transactions on Medical Imaging, Vol.28,  No.1, Jan. 2009, pp.3-16.
[3] I. Frosio, M. Lucchese, N. A. Borghese, A new and reliable Poisson noise estimator for radiographic images, in Proc. ICIAP 2007, Modena (Italy), Sept. 2007.

Back